Physik für Pendler

Etwa 330 Jahre ist es her, seitdem Isaac Newton 1687 seine „axiomata sive leges motus“ veröffentlich hat. Lex prima, lex secunda und lex tertia sind die Grundlagen der klassischen, nicht-relativistischen Mechanik.

Das lex secunda („2. Newtonsches Axiom“), nachdem die auf einen Körper wirkende Kraft gleich der Änderung des Impulses  mit der Zeit ist, ist Grundlage der Impulserhaltung.

Der vorliegende Beitrag erhebt keinen Anspruch auf Vollständigkeit, allenfalls darauf Begeisterung für Mechanik und die Geschichte der Mechanik zu wecken! Es soll auch nicht näher auf Grundlagen der Modellbildung, der numerischen Mathematik,  der Energieerhaltung oder auch des Drehimpulses oder exzentrischen Stoßes eingegangen werden. Dargestellt werden soll ein Auszug aus den Grundlagen unserer Arbeit an einem spielerisch zugänglichen Modell. Es wurde versucht, den Text auch für Nicht-Techniker verständlich zu formulieren. Nichts desto trotz lassen sich technische Zusammenhänge oft gut mit Formeln darstellen, weshalb diese nicht gänzlich vermeidbar waren.

Der Impulserhaltungssatz besagt nun, dass der Gesamtimpuls aller Stoßpartner eines betrachteten Systems vor und nach dem Stoß identisch sein muss. Dies gilt sowohl für elastische Stoßvorgänge (Stoßzahl k = 1) als auch für inelastische (plastische, k = 0), hierzu später mehr. Bei ersteren bleibt die kinetische Energie erhalten, bei letzteren wird eine Umwandlung in eine andere Energieform (z. B. Wärme, „Formänderungsarbeit“ (dem Körper durch Formänderung zugeführte Energie)) stattfinden. In der Realität sind diese Grenzfälle eher  selten anzutreffen. Wirkliche Stoßvorgänge wie z. B. auch Verkehrsunfälle verlangen daher eine Stoßzahl zwischen 0 und 1 (-1 < k < 0 bei Strukturversagen; -1 ist allerdings physikalisch nicht korrekt, deshalb nur hilfsweise).

Anschaulich lässt sich der Impulserhaltungssatz wie folgt herleiten.

Nach Newton (1643 – 1727) gilt bereits:

Die auf einen Körper einwirkende, konstante resultierende Kraft ist gleich dem Produkt aus dessen Masse mal Beschleunigung („dynamisches Grundgesetz“).

Der bei Stoßvorgängen meist sehr kurze Zeitabschnitt  wird nun verbunden mit der Formulierung der Beschleunigung als Ableitung der Geschwindigkeit nach der Zeit

eingeführt. Hieraus

folgt

Das Produkt aus resultierender Kraft auf einen Körper und der Zeit wird als Kraftstoß (in der Unfallrekonstruktion oft auch Stoßantrieb) bezeichnet. Das Produkt aus Masse eines Körpers und seiner Geschwindigkeit nennt man Impuls  – eine vektorielle Größe (gerichtete Größe, Vorzeichen beachten…).

Wirkt keine äußere Kraft, so ist der Kraftstoß gleich Null; der Impuls des Körpers bleibt unverändert. Innere Kräfte ändern den Impuls eines abgeschlossenen Systems nicht; wegen actio = reactio (lex tertia) heben sie sich paarweise auf.

Der Impulserhaltungssatz ist damit für zwei Körper oder allgemein für n Körper wie folgt formuliert:

Wobei  die Geschwindigkeiten der Massenmittelpunkte vor dem Stoß und  die Geschwindigkeiten nach dem Stoß darstellen. Bei konstant bleibenden Massen bedeutet dies, dass die Geschwindigkeit des einen Körpers kleiner und die Geschwindigkeit des anderen größer wird.

Übrigens: die mathematische Formulierung der Impulserhaltung (Impuls und Drehimpuls bzw. Drall) wird nicht Newton, sondern Leonhard Euler (1707 – 1783) zugeschrieben. Deshalb spricht man oft auch von Newton-Euler-Gleichungen.

Es fehlen nun noch die Herren d’Alembert, Lagrange, Bernoulli und Poisson, dann wären  wesentliche Namen der klassischen Mechanik genannt. Das würde hier aber zu weit führen.

Soviel zur Theorie.

Ein gutes Beispiel um sich die Theorie in der Praxis zu veranschaulichen stellt das sogenannte Newton-Pendel dar. Die Anordnung geht zwar auf Edme Mariotte (1620 – 1684) zurück, basiert aber auf den Beobachtungen und den formulierten Gesetzmäßigkeiten von Newton.

Übrigens: ein anderes interessantes Pendel ist das Foucault’sche Pendel (1851) – das hat mit dem Newton-Pendel zwar nichts zu tun, aber wenn man an einem freien Wochenende mal die Erdrotation mit rel. einfachen Mitteln nachweisen muss, sollte man einen solchen Versuch aufbauen.

Abb. 1 Newton-Pendel mit 5 Kugeln

In Abb. 1 ist die Versuchsanordnung zu sehen, die vielen vielleicht bekannt vorkommt. Hier sind 5 Kugeln (hoffentlich möglichst von gleicher Qualität, Form und Werkstoffeigenschaften) in Reihe angeordnet. Lenkt man nun eine oder zwei der außenliegenden Kugeln aus und lässt sie los, so kann man die immer wieder faszinierende Mechanik und deren Gesetzmäßigkeiten beobachten.

Für den Simulanten schreit das geradezu danach, das Experiment am Rechner nachzubilden.

Das haben wir getan!

Und zwar mit der Genauigkeit, die ein handelsüblicher Meterstab beim Vermessen hergibt. Der Kugeldurchmesser wird mit der Schieblehre abgenommen, aus der Dichte von Stahl und dem errechneten Volumen ergibt sich die Masse einer Kugel. Das Trägheitsmoment der Kugel ist praktischerweise um alle drei Achsen identisch und muss nur einmal berechnet werden.

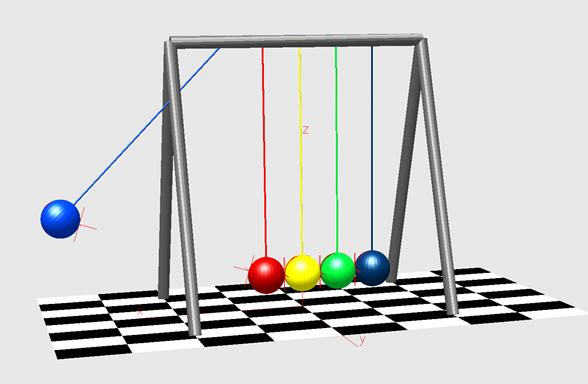
Abb. 2 Mehrkörper-Modell

Die Abb. 2 illustriert das aufgebaute Modell in der Methodik der Mehrkörpersysteme (MKS). Die Mehrkörperdynamik bzw. die Mehrkörpersimulation ist zu unterscheiden von der wohl bekannteren Finite-Elemente-Methode (FEM)! Grundgedanke der MKS ist die Nachbildung von (dynamischen) Systemen aus starren (wo notwendig teils auch flexiblen) Körpern, die den unterschiedlichsten Kräften und Zwängen unterworfen sind. Ziel ist es, das Zeitverhalten (z. B. Bewegungen, Geschwindigkeiten, Beschleunigungen, Kräfte) zu studieren. Der herausragende Vorteil der MKS ist, dass die meisten Modelle sehr geringe Rechenzeiten haben. Das ist Voraussetzung, um bspw. an eine Echtzeit-Anwendung denken zu können (wie z. B. das sog. Einspurmodell im ESP-Steuergerät eines modernen Kfz).

Das hier vorgestellte Modell ist dann gleich ein Beispiel dafür, dass die Rechenzeiten eher in den Bereich einer Kaffeepause gehen statt Richtung Echtzeit (Achtung, Begriff wird oft falsch verwendet); ein wesentlicher Grund hierfür wird später noch genannt.

Vereinfachend werden die Kugeln statt an jeweils 2 Fäden an einem masselosen Fadenpendel aufgehängt. Die Aufhängung wird reibungsfrei mit 1 Drehfreiheitsgrad modelliert.

Die Körper (in diesem Fall Kugeln) werden mit den gewünschten Eigenschaften nachgebildet. Entscheidend sind in diesem einfachen Fall die Kontaktsteifigkeiten und –dämpfungen. Durch Auswahl und Zuweisung entsprechender sogenannter Kraftelemente in der Software wird dafür gesorgt, dass der Zusammenstoß zweier benachbarter Kugeln erkannt und entsprechend behandelt wird. D.h. durch Aufbau von Kräften entsprechend den hinterlegten Kraft-Weg- bzw. Kraft-Geschwindigkeits-Zusammenhängen. Ebenso berücksichtigt werden muss, dass die Kugeln nicht immer an der gleichen Stelle zusammenstoßen müssen, der Kontaktpunkt kann also über die Kugeloberfläche wandern. Für die Kontaktpaarung Stahl – Stahl werden natürlich sehr hohe Steifigkeiten verbunden mit niedrigen Dämpfungen benötigt. Eine solche Parametrierung führt erfahrungsgemäß zu rel. hohen Rechenzeiten (Schrittweiten müssen sehr klein gewählt werden, System sehr „steif“); das soll hier aber nicht das Thema sein.

Die Grundlagen für die Berechnung eines solchen Kontaktes („Hertzsche Pressung“, 1881) wurden übrigens durch Heinrich Hertz (1857 – 1894) gelegt, der v.a. aufgrund seines Nachweises der Existenz elektromagnetischer Wellen bekannt ist.

Eine Steifigkeit c ist als ein Zusammenhang zwischen einer Kraft F und einem Weg s in der Form

  in der Einheit   

definiert.

Die erste Kugel (hellblau in Abb. 2) wird um PI/4, also 45° ausgelenkt. Aus dieser Anfangsbedingung heraus wird der Solver (Löser der in Matrizenform vorliegenden Bewegungsdifferentialgleichungen durch Zeitintegration) gestartet, um das Zeitverhalten des Systems aufzulösen.

In der Zwischenzeit kann man sich schon mal (analytisch) Gedanken machen, mit welcher Geschwindigkeit wohl die Kugel 1 auf die Kugel 2 (rot) auftrifft.

Es hilft eine einfache Energiebilanz nach dem Schema

Die Höhendifferenz  ergibt sich trigonometrisch mit dem Winkel  und der bekannten Pendellänge , der Differenz z₁ zwischen den beiden Längenmaßen aus

folgt

und .

Der Energieansatz ergibt nach Wegkürzen der Masse die Geschwindigkeit der Kugel 1 vor dem Stoß:

Die Kugel 1 bringt demnach folgenden Impuls  mit:

Hinweis:

In den nachfolgenden Diagrammen ist die x-Achse immer die Zeitachse und die y-Achse die Geschwindigkeitsachse bzw. die Kraftachse.

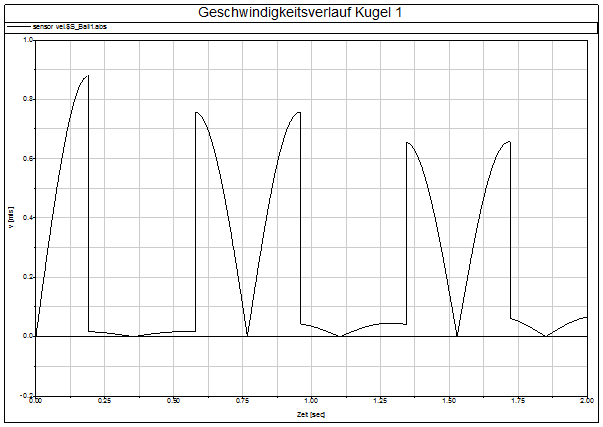
Abb. 3 Geschwindigkeitsverlauf Kugel 1

Wir vergleichen mit den Ergebnissen der MKS-Rechnung, siehe Abb. 3. Die Kugel startet logischerweise bei  und erreicht ihre maximale Geschwindigkeit am Nulldurchgang, wo sie dann schlagartig durch Kugel 2 abgebremst wird. Das Maximum bei knapp  beträgt relativ genau  (im Folgenden mit  bezeichnet) – wie oben analytisch hergeleitet. Die Kugel wird diese Geschwindigkeit nicht mehr erreichen – in realen Systemen gibt es immer Dämpfung, die Energie „auffrisst“ oder technischer formuliert in eine andere Energieform umwandelt (z. B. Wärme). Die Struktureigendämpfung von Stahl wurde mit 2 % angenommen (der Wert berechnet sich überschlagsmäßig aus der bewegten Masse und der verwendeten Steifigkeit).

Dies zeigt dann auch deutlich Abb. 4. Dort ist im Vergleich der Geschwindigkeitsverlauf von Kugel 1 (links außen) und Kugel 5 (rechts außen) dargestellt.

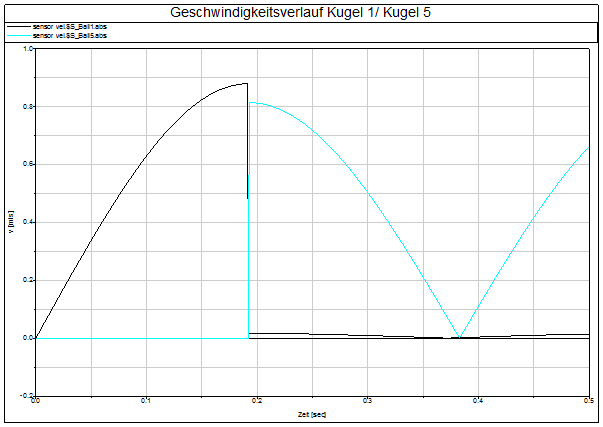
Abb. 4 Geschwindigkeitsverlauf Kugel 1 / Kugel 5

Die Kugel 5 (hellblau) erreicht beim erstmaligen Kontakt nicht das Geschwindigkeitsniveau von Kugel 1 (schwarz). Kugel 5 wird also beschleunigt, während Kugel 1 fast auf 0 m/s abgebremst wird. Was passiert aber mit den Kugeln 2, 3 und 4?

Diese laufen mit derselben Geschwindigkeit der Kugel 1 (nahe Null) mit. Das ist neben der Dämpfung auch der hauptsächliche Grund dafür, dass nicht der gesamte, eingebrachte Impuls der Kugel 1 über alle mittleren Kugeln an die Kugel 5 weitergegeben wird. Ein Teil des Anfangsimpulses bleibt also „hängen“. Der Impulserhaltungssatz wird nicht verletzt.

Näherungsweise lassen sich aus folgender Abb. 5 die Geschwindigkeiten der Kugel 1 vor und die der Kugeln 1 – 5 nach dem Stoß ablesen:

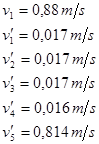
Es gilt der Impulserhaltungssatz (die Massen aller Kugeln werden als identisch angenommen):

Da alle 5 Kugeln  einen postkollisionären Impuls abbekommen muss bei gerechtfertigter Annahme der Massenerhaltung der Kugeln über der Zeit (was wir hoffen wollen…; Massen können sich aber auch ändern wie z.B. bei Raketen, wo der Treibstoff im Verhältnis zum Gesamtgewicht beträchtlich ist und mit zunehmender Zeit weniger wird, formuliert durch Konstantin Ziolkowski 1903 in der sog. „Rakentengleichung“. Man kann aber auch auf dem Boden bleiben und könnte sich ein Beispiel aus der Unfallrekonstruktion vorstellen, wie z.B. ein herausgerissener Motorblock infolge einer kapitalen Kollision) gelten:

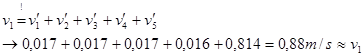
Die vorkollisionären Geschwindigkeiten sind aus der Anschauung heraus auf 0 zu schätzen – die Terme fallen weg. Die Ergebnisse der Simulation sind also plausibel.

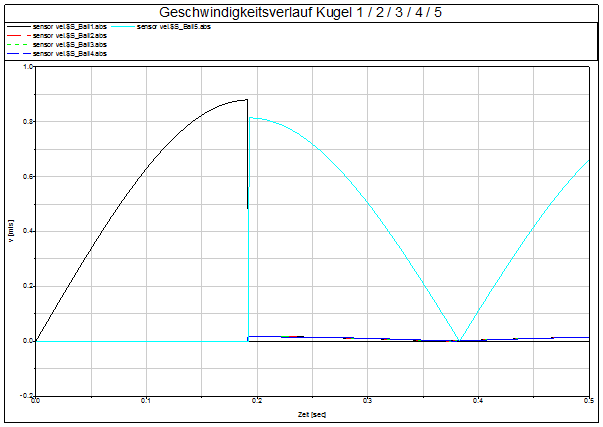
Abb. 5 Geschwindigkeitsverlauf aller Kugeln

Der nahezu gleichzeitige und verzugslose Anstieg der Geschwindigkeit der Kugel 5 von 0 auf 0,81 m/s könnte auch als sogenannter Dirac-Stoß (zeitlich gesehen zunächst zwischen Kugel 1 und Kugel 2, anschließend aber auch alle folgenden Kontakte) interpretiert werden. Schauen wir uns dazu folgende Abb. 6 an.

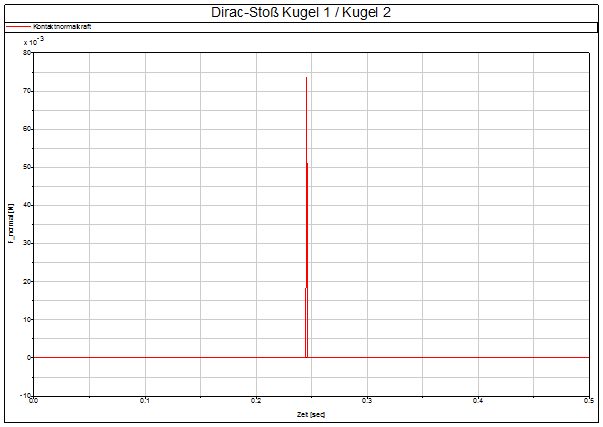
Abb. 6 Dirac-Stoß

Die Kontaktnormalkraft wird in infinitesimaler Zeit quasi unendlich groß, d.h. die Kollisionsdauer ist sehr kurz. Hier offenbart sich ein bekanntes „Problem“ der numerischen Simulation. In Abb. 6 ist ein sehr schmaler peak zu sehen, theoretisch müsste dieser  kurz vor  (vgl. Abb. 5) beginnen. Der Kontakt selbst wird zwar erkannt, wegen der sehr hohen Steifigkeit und der äußerst geringen Kontaktdauer darf die Kontaktkraft jedoch nicht verwendet werden. Die errechnete Kraftamplitude in Abb. 6 ist demnach mit Vorsicht zu genießen! Für die Zeitauflösung der eigentlichen Kollisionsphase in Kompression und Restitution gilt gleiches!

Die Stoßkraft ist also nicht definiert (Stichwort Stoßhypothese nach Newton bzw. Poisson).

In der Systemtheorie dynamischer Systeme wird ein derartiges Ereignis auch als Singularität bezeichnet.

Wollte man nun sämtliche Geschwindigkeiten analytisch bestimmen, so müsste zunächst postuliert werden, dass die Stöße nicht gleichzeitig sondern kurz nacheinander stattfinden. Ansonsten stünden nur 2 Gleichungen (Impulssatz und Energieerhaltung) für 5 Kugeln und deren unbekannte Geschwindigkeiten zur Verfügung.

Alternativ könnte man statt der Energieerhaltung auch die Stoßzahl mit ins Spiel bringen.

Die Stoßzahl  bezeichnet in Prinzip ein Verhältnis der Geschwindigkeitsdifferenzen der beteiligten Körper vor und nach dem Stoß.

Um nun die Stoßzahl für die Kugelkontaktpaarung zu ermitteln, lässt man einfach die Kugeln 3 – 5 komplett aus dem Spiel, so dass Kugel 2 frei wegschwingen kann:

Abb. 7 Geschwindigkeitsverlauf Kugel 1 / 2 (ohne Kugeln 3/4/5)

Die Stoßzahl ergibt sich aus den abgelesenen Geschwindigkeiten zu

Das liegt nahe am vollelastischen Stoß (wie bspw. auch bei Billardkugeln), für den gilt:

Nun ließe sich mit der errechneten Stoßzahl aus dem Einzelstoß-Experiment die Geschwindigkeit der Kugel 5 nach dem Stoß errechnen.

Selbstverständlich ist die Rechnung fehlerbehaftet, denn die Impulse der Kugeln 2, 3 und 4 sind nicht berücksichtigt worden.

Subtrahiert man diese von , so kommt man mit

auf den zuvor simulatorisch ermittelten Wert.

Abschließend sind 2 kurze Videos abgelegt, die die Stoßvorgänge einmal für die Anfangsbedingung „eine ausgelenkte Kugel“ und zum zweiten „zwei ausgelenkte Kugeln“ illustrieren sollen.

Wie darin zu sehen, verhalten sich die anderen Kugeln wie bereits erwähnt nicht gänzlich still, an den mittleren Kugeln bleiben also Impulse „hängen“.

Hierbei spielen auch die Spalte zwischen den Kugeln eine Rolle. Diese sollen sicherstellen, dass die Stöße voneinander unabhängig stattfinden, d.h. zeitlich nacheinander, wenn auch nur Sekundenbruchteile. Diese Forderung ist notwendig, wenn das Kugelstoß-Pendel „ordentlich“ funktionieren soll.

Die Luftspalte haben dann jedoch zur Folge, dass nicht mehr nur in Normalrichtung zwischen den Kugeln Kräfte entstehen, sondern kleine Kräfte auch in Tangentialrichtung.

VIDEO 1

VIDEO 2

Fazit:

Ein Spielzeug mit ein paar Kugeln, das jedoch bei näherer Betrachtung nicht mehr so trivial daherkommt, wie man vielleicht denken könnte.

Die so einfach erscheinende Mechanik fasziniert immer wieder und die in den letzten Jahrhunderten geschaffenen Grundlagen sind nach wie vor unerlässlich. Die Erkenntnisse, die die Herren Newton und Co. damals ohne Digitalrechner gewannen sind heute immer noch gültig, auch wenn erst Einstein die Newtonsche Mechanik quasi zum Grenzfall der Relativitätstheorie „degradierte“.

Die Modellbildung hat ihre Tücken und nur bei Kenntnis der in der Software programmierten Gesetzmäßigkeiten sind deren Grenzen  ersichtlich und die Ergebnisse lassen sich entsprechend bewerten. 

Übrigens: Schon lange bevor Newton & Co. über Impulsen grübelten, gab es erste, jedoch wohl eher unfreiwillige (gut, könnte auch eine frühe Form von Billard gewesen sein ;-) Versuche dazu. Beteiligt waren die Erde und der ein oder andere Meteorit. Die These amerikanischer Forscher um Marc Boslough ist nun, dass die durch den Einschlag eines Meteoriten auf der Südhalbkugel erzeugte Druckwelle am Antipoden (auf der gegenüberliegenden Seite) noch ausreichend Energie inne hat, um Vulkane zu erzeugen.  Der Meteorit soll einen Durchmesser von etwa 8 km gehabt haben; durch den Impuls beim Stoß läuft eine Front seismischer Wellen mit ~ 13.000 km/h durch die Erdkugel, bis sie ca. 1,5 h später auf der anderen Seite ankommt (dort kann dann der Impuls nicht weitergegeben werden, weil keine 2. Erdkugel am Pendel hängt). Simulatorisch konnte man das sogar nachweisen, hierzu langt aber eine MKS-Starrkörper-Rechnung auf der workstation nicht mehr aus. Es müssen kontinuumsmechanische Berechnungen (FEM) mit einer nahezu unvorstellbar großen Anzahl von Freiheitsgraden durchgeführt werden.

In der Rechtsmedizin oder auch aus Verkehrsunfällen ist der Effekt der Antipoden-Veränderung als Contre-Coup-Mechanismus bekannt. Wird bspw. ein durch eine Frontalkollision nach vorne fallender Schädel durch ein Hindernis wie ein Lenkrad abrupt abgebremst, so soll nicht nur auf der Seite der Einwirkung (vorne), sondern auch hinten am Kopf eine Hirnschädigung (innen, durch Kontakt zwischen Hirnmasse und Schädel) zu erwarten sein.

In diesem Sinne: „again what learned“ frei nach Loddar M.

Anmerkung:

Für viele der hier verwendeten Begrifflichkeiten, Personen oder Sachverhalte sind in wikipedia mittlerweile Einträge vorhanden. Die Beiträge sind meist verständlich formuliert und die (wissenschaftliche) Qualität ist meist auf hohem Niveau. Für weiteres Verständnis oder tieferes Interesse lohnt sich also durchaus ein Klick dorthin.

Hinweis zur Darstellung: die Formeln werden mit dem Mozilla Firefox wesentlich besser dargestellt als mit dem MS Internet Explorer. Deswegen im Zweifelsfalle den Feuerfuchs verwenden (empfiehlt sich sowieso...).

ZURÜCK